평면 위 두 점 사이의 거리
피타고라스의 정리를 사용하여 두 점 사이의 거리를 구할 수 있습니다.
d = \sqrt{(a_{1}+a_{2})^2+(b_{1}+b_{2})^2}그러나 특정 두 점 사이의 거리를 구할 때 평면 위의 피타고라스 공식을 사용한다면 구형인 지구 위에서 거리가 멀어질수록 큰 오차가 발생합니다.
이 오차를 어떻게 바로잡을 수 있을까요?
구형 위 두 점 사이의 거리
구형 위에서 생기는 두 점 간의 거리 오차를 조정하기 위하여 한 점의 정확한 위치를 나타낼 위도와 경도가 필요합니다.
위도 (Latitude)
위도는 지구의 적도를 기준으로 그린 선에 평행하는 선으로 극지방으로 갈수록 그 길이가 작아집니다. 위도 간 거리는 지구 어디에서나 동일하게 적용됩니다. 이것은 사각형 위에 균일한 거리로 평행선을 그린 것과 같습니다.
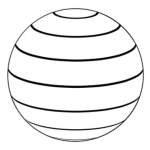
경도 (Longitude)
경도는 지구의 남극과 북극을 잇는 선으로 모두 동일한 값을 가집니다. 경도 간 거리는 위도가 커질수록 작아집니다. 극지방으로 올라갈수록 원의 반지름은 작아지기 때문입니다.
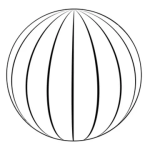
위도와 경도의 기본 단위는 도 라고 읽으며, 우리가 시계를 읽는 방법과 동일한 분, 초 단위가 존재합니다.
두 점 사이의 거리
두 점 사이의 거리는 Haversine 공식을 이용하여 계산할 수 있습니다. 6371은 지구의 반지름입니다.
\varphi_1 = lat_1\cdot\pi\div180,\\ \varphi_2 = lat_2\cdot\pi\div180,\\ \Delta\lambda = (lon_2-lon_1) \cdot\pi\div180,\\ R = 6371\\ \\ m_1=sin \varphi_1 \cdot sin \varphi _2,\\ m_2 = cos\varphi _1 \cdot cos\varphi _2 \cdot cos \Delta\lambda,\\ \\ d = acos( m_1 + m_2) \cdot R
지도에서 특정 지점의 위도와 경도값을 알아낼 수 있으며, 스마트폰의 GPS를 이용하여 사용자의 위도와 경도값을 구할 수 있습니다.
우리는 특정 지점과 사용자 각 두 점의 위도와 경도를 Haversine 공식에 대입하여 떨어져 있는 거리를 계산할 수 있게 됩니다.
다음은 서울시청과 광화문 간의 거리를 구하는 예제입니다.
- 서울시청 : 위도 37.5666791, 경도 126.9782914
- 광화문 : 위도 37.5701134, 경도 126.9767776
PHP
<?php
// 서울시청과 광화문의 위도와 경도 값
$start = array(37.5666791, 126.9782914);
$end = array(37.5701134, 126.9767776);
// Haversine 공식으로 거리 계산
function getDistance($foo, $bar) {
$lat1 = $foo[0];
$lon1 = $foo[1];
$lat2 = $bar[0];
$lon2 = $bar[1];
$theta = $lon1 - $lon2;
$d = sin(deg2rad($lat1)) * sin(deg2rad($lat2)) + cos(deg2rad($lat1)) * cos(deg2rad($lat2)) * cos(deg2rad($theta));
$d = rad2deg(acos($d));
$mile = $d * 60 * 1.1515;
$meter = $mile * 1609.344;
return $meter;
}
// 서울시청과 광화문 간의 거리 출력
$d = getDistance($start, $end);
echo "서울시청과 광화문 간 거리는 약 " . round($d, 2) . "m 입니다.";
INAS의 블LOG에 오신 것을 환영합니다
